A. Cell motility
This research concerns the development of models for surface growth,
as they apply to the motility of certain classes of biological cells, such as
fish epidermal keratocytes. Surface growth occurs when material is
added to or removed from the surface of the body. The theoretical challenges
of surface growth stem from the fact that the resulting motion is generally
non-material and needs to be tracked relative to an ever evolving reference
configuration. Furthermore, one needs to track the dynamics of several
motility-relevant protein species, which affects the stress, as well as the
tractions developed between the cell and the substrate.
On the computational side, finite element methods need to be suitably
formulated to account for the growth and resorption at the surface.
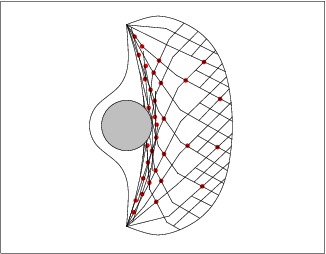
The following image depicts the actin network (mesh) and the myosin-II (red dots) in a motile fish epidermal keratocyte.
Related Publications:
B. Bone strength
This work, done jointly with Professor T.M. Keaveny, concerns the
detailed modeling of bone structures, especially of trabecular type,
and the estimation of strength from a combination of experimental measurement
of the bone topology and computer simulation of the stress due to habitual or
accidental loading. A further area of interest includes bone adaptation
through stress- or strain-induced volumetric growth and resorption.
The following image depicts a high-resolution finite element model of trabecular bone obtained by converting a CT-scan into a mesh of hexahedral elements.

Related Publications: