A. Shape-memory alloys
This research concerns the combined experimental, analytical and
computational study of superelasticity and the shape-memory effect
in metal alloys, especially NiTi and CuZnAl. The experimental portion of this
work is done in collaboration with
Professor R.O. Ritchie.
The following image shows the experimental setup for bi-axial (tension-torsion) loading of thin NiTi tubes under displacement control, slow loading rates and essentially isothermal conditions:

Related Publications:
Short course material:
P. Papadopoulos.
``Constitutive Modeling and Simulation of the Superelastic Effect in
Shape-Memory Alloys'' , CISM, Udine, July 2005.
B. Estimation of material properties using molecular dynamics
The purpose of this research is to estimate mechanical and thermal
properties of materials using methods of statistical mechanics, as implemented
computationally within the framework of molecular dynamics techniques.
Properties of particular interest include elasticities in metals and alloys,
as well as thermal conductivities in microscale systems.
The following snapshot shows an instance of a simple two-dimensional molecular dynamics calculation for Cu under constant temperature:

Related Publications:
C. Fabric materials
This research concerns the modeling and simulation of fabric materials
used in a wide array of applications ranging from lightweight
ballistic shields (e.g., body armor, aircraft fuselage barriers) to
high-strength flexible systems (e.g., parachutes) to everyday clothing
manufacture. Particular emphasis is given to special-purpose materials such as
Kevlar and Zylon, which exhibit high strength-to-weight ratio.
The following image shows the numerical simulation of a push-test on a clamped fabric sheet made of Kevlar:

Related Publications:
D. Multiscale modeling of materials
This research focuses on the coupling of length and time scales using atomistic and continuum methods. Emphasis is placed on both theoretical and computational aspects with application to solids.
Related Publications:
i>K.K Mandadapu, A. Sengupta and P. Papadopoulos.
``A Homogenization Method for
Thermomechanical Continua using Extensive Physical Quantities''
,
Proc. Royal. Soc. London A., 468, pp. 1696-1715, (2012).
E. Computational plasticity
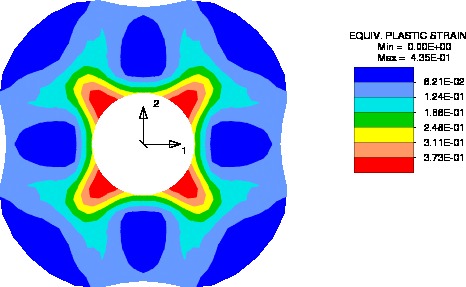
This research focuses on the use of finite element-based methods in the analysis of problems of infinitesimal and finite plasticity within the context of the strain-space formulation. Research in infinitesimal plasticity concentrates on issues of stability and accuracy of the algorithms used in the integration of the underlying differential/algebraic equations, as well as solveability issues concerning non-associative models. Research in finite plasticity concerns the derivation and numerical implementation of theoretically sound and physically plausible models for analysis of the elastic-plastic response of metallic bodies that undergo finite deformations.The following image shows the deformed shape and the equivalent plastic strain of an initially curcular flange which is deep-drawn by pulling the inner circular boundary inwards. Note the loss of axisymmetry, which is due to the orthotropic yield condition:
Related Publications: